前回までのお話はこちら
共面条件
4点が同一平面上に存在するとき,点の位置を1次独立なベクトル2つで表すことができる.$s$,$t$をそれぞれ実数とすると,
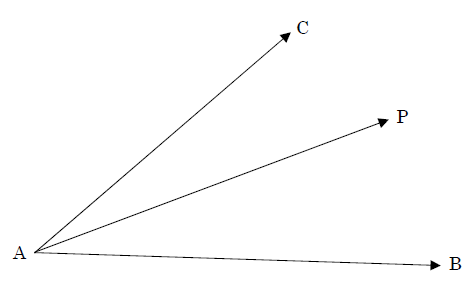
$\overrightarrow{AP}=s\overrightarrow{AB}+t\overrightarrow{AC}$
と表すことができる.始点変換を行うと,
$\overrightarrow{OP}-\overrightarrow{OA}=s(\overrightarrow{OB}-\overrightarrow{OA})+t(\overrightarrow{OC}-\overrightarrow{OA})$
⇔ $\overrightarrow{OP}=(1-s-t)\overrightarrow{OA}+s\overrightarrow{OB}+t\overrightarrow{OC}$
共線条件は,主に空間の位置ベクトルの問題で,同一平面に4点が存在する→立式する→共線条件ででた式と連立する という流れで解き進めるのに必要となる.
【おまけ】
点Pが平面ABC上にあるとき,$s$,$t$の値に関係なく$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$の係数和は1になる.
これを証明に利用することがあるので覚えておこう.点Pが$\overrightarrow{OP}=p\overrightarrow{OA}+q\overrightarrow{OB}+r\overrightarrow{OC}$と表されている場合,$p+q+r=1$ならば,点Pは平面ABC上に存在するといえる.
例題
四面体OABCの辺OAを$1:1$に内分する点をD,辺OBを$2:1$に内分する点をE,辺OCを$1:2$に内分する点をF,辺ABを$1:2$に内分する点をPとする.また,線分CPを$t:(1-t)$に内分する点をQとし,平面DEFと線分OQとの交点をRとする.ただし,$0<t<1$とする.以下の問いに答えよ.
(1) $\overrightarrow{OQ}$を$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$および$t$を用いて表せ.
(2) 点Rが線分OQを$2:3$に内分するとき,$t$の値を求めよ.
【日本女大 2020】
解き方
➀図を描く
➁点に関する情報を探し立式する(共線条件、共面条件)
➂点に関しての式を基準ベクトルだけの式で表す.
④連立方程式を解く.
解答
(前段階として共線条件を用いて以下情報を集める)
$\overrightarrow{OA}=2\overrightarrow{OD}$
$\overrightarrow{OB}=\displaystyle\frac{3}{2}\overrightarrow{OE}$
$\overrightarrow{OC}=3\overrightarrow{OF}$
(1) 3点C,P,Qは同一直線上に存在するので,
$\overrightarrow{CQ}=t\overrightarrow{CP}$
⇔$\overrightarrow{OQ}-\overrightarrow{OC}=t(\overrightarrow{OP}-\overrightarrow{OC})$
⇔$\overrightarrow{OQ}=t\overrightarrow{OP}+(1-t)\overrightarrow{OC}・・・➀$
・$\overrightarrow{OP}$に関して.
3点A,B,Pは同一直線上に存在するので,
$\overrightarrow{AP}=\displaystyle\frac{1}{3}\overrightarrow{AB}$
$\overrightarrow{OP}-\overrightarrow{OA}=\displaystyle\frac{1}{3}(\overrightarrow{OB}-\overrightarrow{OA})$
$\overrightarrow{OP}=\displaystyle\frac{2}{3}\overrightarrow{OA}+\displaystyle\frac{1}{3}\overrightarrow{OB}・・・➁$
➀に➁を代入すると,
$\overrightarrow{OP}=\displaystyle\frac{2}{3}t\overrightarrow{OA}+\displaystyle\frac{1}{3}t\overrightarrow{OB}+(1-t)\overrightarrow{OC}$ (答)
(2)3点O,Q,Rは同一直線上に存在するので,
$\overrightarrow{OR}=\displaystyle\frac{2}{5}\overrightarrow{OQ}$
⇔$\overrightarrow{OR}=\displaystyle\frac{2}{5}(\displaystyle\frac{2}{3}t\overrightarrow{OA}+\displaystyle\frac{1}{3}t\overrightarrow{OB}+(1-t)\overrightarrow{OC})$
⇔$\overrightarrow{OR}=\displaystyle\frac{4}{15}t\overrightarrow{OA}+\displaystyle\frac{2}{15}t\overrightarrow{OB}+\displaystyle\frac{2}{5}(1-t)\overrightarrow{OC}・・・➂$
また,4点D,E,F,Rは同一平面上に存在するので,実数$l$,$m$を用いて,
$\overrightarrow{DR}=l\overrightarrow{DE}+m\overrightarrow{DF}$
⇔$\overrightarrow{OR}-\overrightarrow{OD}=l(\overrightarrow{OE}-\overrightarrow{OD})+m(\overrightarrow{OF}-\overrightarrow{OD}$
⇔$\overrightarrow{OR}=(1-l-m)\overrightarrow{OD}+l\overrightarrow{OE}+m\overrightarrow{OF}・・・④$
➂④を連立させると,$t=\displaystyle\frac{3}{7}$ (答)


コメント