最短経路

問題

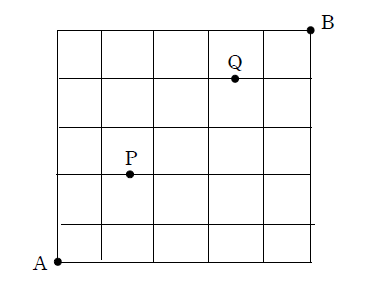
　上の図のような道がある．

(1)　地点Aから地点Bまでの最短な道順は何通りか．

(2)　地点Pと地点Qが通れないとき，最短な道順は何通りか．

【中部大学　2020　(文言変更)】

解答

(1)　→に5回，↑に5回移動すればよい．同じものを含む順列と考えると，

$\dfrac{10!}{5!\cdot5!}=\dfrac{10\cdot9\cdot8\cdot7\cdot6}{5\cdot4\cdot3\cdot2\cdot1}=252$通り

(2)

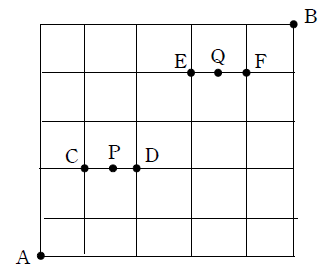
　上記のように点C、D、E、Fを設定する．

(A)　Pを通るとき，特にA→C→D→Bのとき

$\dfrac{3!}{2!1!}\cdot1\cdot\dfrac{6!}{3!}=60$通り

(B)　Qを通るとき，特にA→E→F→Bのとき

$\dfrac{7!}{3!4!}\cdot1\cdot\dfrac{2!}{1!}=70$通り

(C)　PとQを通るとき，特にA→C→D→E→F→Bのとき

$\dfrac{3!}{1!}\cdot1\cdot\dfrac{3!}{1!}\cdot1\cdot\dfrac{2!}{1!}=18$通り

(A)～(C)よりPまたはＱを通るものは

$60+70-18=112$通り

よって，P，Qが通れないときの最短経路は

$252-112=140$通り