前回のお話はこちらから
さて,イメージのお話は終わったので,ここでは重要な公式を2つ紹介したいと思います.平面の位置ベクトルの問題に対しては,これらの公式があれば解けます。(*内分公式などを知っていれば計算が楽になります・・・)ここでは,全ての公式を忘れて,取り組みましょう!!!
私の中で位置ベクトルの問題を解くのに必要な公式は3つだけですよ!
始点変換
$\overrightarrow{AB}=\overrightarrow{○B}-\overrightarrow{○A}$
[使い方] ある問題で・・・
(1) $\overrightarrow{BQ}$を$\overrightarrow{OA}$,$\overrightarrow{OB}$を用いて表せ.
とあったとする.この場合,$\overrightarrow{BQ}$を$\overrightarrow{BQ}=\overrightarrow{OQ}-\overrightarrow{OB}$と始点を$O$に揃えることができる.この後,点Qに関する情報を次に紹介する公式を用いて,解き進めることになる.
位置ベクトルの問題を解くときには,式中のベクトルをすべて基準ベクトルで表すことを意識すればよい.(基準ベクトルは基本的には問題で指定される)
共線条件(3点同一直線上条件)
始点変換と、この共線条件があれば平面ベクトルの問題は解き進めることができる.
それでは紹介していこう.

3点が同一直線上にあるとき,点の位置をベクトルと実数で表すことができる.$k$を実数とすると,
$\overrightarrow{AP}=k\overrightarrow{AB}$
と表すことができる.また,$\overrightarrow{OA}$,$\overrightarrow{OA}$を基準ベクトルとすると,始点変換の公式を利用することで,
$\overrightarrow{OP}-\overrightarrow{OA}=k(\overrightarrow{OB}-\overrightarrow{OA})$
⇔ $\overrightarrow{OP}=(1-k)\overrightarrow{OA}+k\overrightarrow{OB}$
と点Pの位置を基準ベクトルを用いて,表すことができた.
例題
△OABにおいて,辺OAを2:1に内分する点をC,辺OBの中点をDとし,線分ADとBCの交点をPとする.$\overrightarrow{OA}=\overrightarrow{a}$,$\overrightarrow{OB}=\overrightarrow{b}$とするとき,
$\overrightarrow{OP}=(ア)\overrightarrow{a}+(イ)\overrightarrow{b}$
と表される.
【東京工芸大 2020 一部抜粋】
簡単な指針
解き進め方としては
➀ 簡単な図を描く(比が分からないところは適当でOKです)
➁ 図から3点が同一直線に存在する点に関する情報を集める(共線条件)
(問題で与えられる点の情報を全て集めていくため,比が与えられた点から解くのがオススメ.比が分からないところは文字で置く.)
➂ ➁で立てた式を基準ベクトルに直す作業を行う(始点変換)
④ ➁,➂を繰り返す行う
解き方
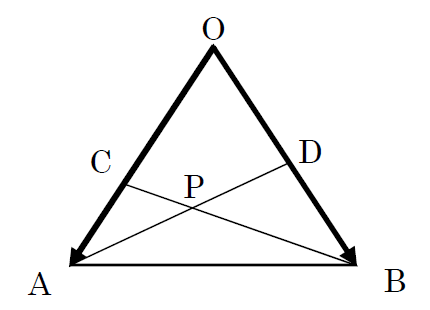
3点O,A,Cが同一直線上に存在するので,共線条件より,
$\overrightarrow{OC}=\displaystyle\frac{2}{3}\overrightarrow{OA}$
となる.また,3点O,B,Dが同一直線上に存在するので,共線条件より,
$\overrightarrow{OD}=\displaystyle\frac{1}{2}\overrightarrow{OB}$
となる.
3点A,D,Pが同一直線上に存在するので,$s$を実数とすると,
$\overrightarrow{AP}=s\overrightarrow{AD}$
$\overrightarrow{OP}-\overrightarrow{OA}=s(\overrightarrow{OD}-\overrightarrow{OA})$ (始点変換)
$\overrightarrow{OP}=s\overrightarrow{OD}+(1-s)\overrightarrow{OA}$
$\overrightarrow{OP}=\displaystyle\frac{1}{2}s\overrightarrow{OB}+(1-s)\overrightarrow{OA}$
$\overrightarrow{OP}=(1-s)\overrightarrow{OA}+\displaystyle\frac{1}{2}s\overrightarrow{OB}・・・➀$
同様に,3点B,C,Pが同一直線上に存在するので,$t$を実数とすると,
$\overrightarrow{BP}=t\overrightarrow{BC}$
$\overrightarrow{OP}-\overrightarrow{OB}=t(\overrightarrow{OC}-\overrightarrow{OB})$ (始点変換)
$\overrightarrow{OP}=t\overrightarrow{OC}+(1-t)\overrightarrow{OB}$
$\overrightarrow{OP}=\displaystyle\frac{2}{3}t\overrightarrow{OA}+(1-t)\overrightarrow{OB}・・・➁$
$\overrightarrow{OA}$,$\overrightarrow{OB}$は1次独立なので,➀,➁より,
$1-s=\displaystyle\frac{2}{3}t・・・➂$
$\displaystyle\frac{1}{2}s=1-t・・・④$
➂,④より
$s=\displaystyle\frac{1}{2}$
$t=\displaystyle\frac{3}{4}$
となる.これらより,
$\overrightarrow{OP}=\displaystyle\frac{1}{2}\overrightarrow{OA}+\displaystyle\frac{1}{4}\overrightarrow{OB}$
よって、
$\overrightarrow{OP}=\displaystyle\frac{1}{2}\overrightarrow{a}+\displaystyle\frac{1}{4}\overrightarrow{b}$
となる.よって$(ア)\displaystyle\frac{1}{2} (イ)\displaystyle\frac{1}{4}$
コメント
おそらく,学校で習うとき,この手の問題は$AP:PD=(1-s):s$,$CP:PC=(1-t):t$と置くことになるだろう.ただ,いつ置くのかという判断が難しい。また,なんでもかんでも文字で置くと,必要以上に多くの連立方程式を解くことになる.そのため,私は今回のように使う公式を2つだけにして平面の位置ベクトルの問題を解くようにしている.



コメント