どこまで覚えたらよい・・?
結論から申し上げます.人によって様々です.おいっ!!って突っ込まれそうですね。。その理由をあげておくと,
・共通テスト(旧センター試験)では時間との勝負になるので,覚えておくほうが早く解ける
その一方で,
・加法定理の証明が入試で出題された(1999年 東京大学)
ということがあります.そのため,一概には言えない.と言わざるを得ないんですよね。。。。
ある程度区切りをつけておくとしたら,➀旧帝大を受験する人は公式の証明を導出できるレベルまで ➁共通テスト・私立・地方国公立大学を受ける人は,ほぼすべての公式を覚えておく.というのが目安かなと考えています.(公式の導入の仕方を覚えていけばよいものは後述)
三角比 公式
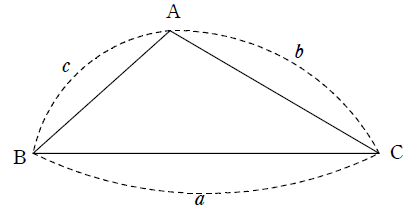
・正弦定理 (覚える!)
$\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=2R$
・余弦定理 (覚える! 三平方の定理の派生)
$a^2=b^2+c^2-2bc\cos A$
・三角形の面積 (覚える!)
$S=\dfrac{1}{2}bc\sin A=\dfrac{1}{2}ca\sin B=\dfrac{1}{2}ab\sin C$
三角関数 公式
・加法定理 (覚える! 人によっては導出できるように)
$\sin(\alpha±\beta)=\sin\alpha\cos\beta±\cos\alpha\sin\beta$
$\cos(\alpha±\beta)=\cos\alpha\cos\beta∓\sin\alpha\sin\beta$
$\tan(\alpha±\beta)=\dfrac{\tan\alpha±\tan\beta}{1∓\tan\alpha\tan\beta}$
・2倍角公式 (加法定理から導出可だが、覚えておいたほうが楽)
$\sin2\alpha=2\sin\alpha\cos\alpha$
$\cos2\alpha=\cos^2\alpha-\sin^2\alpha$
$=2\cos^2\alpha-1$
$=1-2\sin^2\alpha$
$\tan2\alpha=\dfrac{2\tan\alpha}{1-\tan^2\alpha}$
・半角公式 (sin,cosはcosの2倍角公式から導出可,tanは$\tan\theta=\dfrac{\sin\theta}{\cos\theta}$より)
↑の半角公式は数学IIIを使う受験生は暗記しておいた方が良いかもしれません。。。
$\sin^2\dfrac{\alpha}{2}=\dfrac{1-\cos\alpha}{2}$
$\cos^2\dfrac{\alpha}{2}=\dfrac{1+\cos\alpha}{2}$
$\tan^2\dfrac{\alpha}{2}=\dfrac{1-\cos\alpha}{1+\cos\alpha}$
三角関数の性質
$\sin (-\theta)=-\sin\theta$ ☜下の項目で求めます
$\cos (-\theta)=\cos\theta$
$\tan (-\theta)=-\tan\theta$
$\sin(\pi±\theta)=∓\sin\theta$ ☜下の項目で求めます
$\cos(\pi±\theta)=-\cos\theta$
$\tan(\pi±\theta)=±\tan\theta$
$\sin(\dfrac{\pi}{2}±\theta)=\cos\theta$
$\cos(\dfrac{\pi}{2}±\theta)=∓\sin\theta$
$\tan(\dfrac{\pi}{2}±\theta)=∓\dfrac{1}{\tan\theta}$
加法定理の利用でややこしい暗記事項を避ける
$\sin (-\theta)=\sin(0-\theta)=\sin 0\cos\theta-\cos0\sin\theta=-\sin\theta$
$\sin(\pi±\theta)=\sin\pi\cos\theta±\cos\pi\sin\theta=\cos\theta$
他の項目でも使えます!その他,積→和,和→積もあります.これらも数学IIIを使う方が出会う確率が非常に高いです。。。今日はここまでで!

コメント