関数が最大値をとるときのx

問題

　関数$y=\displaystyle\frac{x^2+x}{e^x} (x≧0)$が最大値をとるときの$x$の値を求めよ．ただし，$e$を自然対数の底とする．

解答

(1)　$y=\displaystyle\frac{x^2+x}{e^x}$より，

　　$y’=\displaystyle\frac{(2x+1)e^x-(x^2+x)e^x}{(e^x)^2}=-\displaystyle\frac{x^2-x-1}{e^x}$

　よって，$x≧0$での増減は下表のようになる．

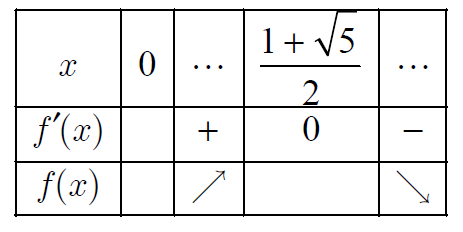
　求める$x$の値は$\displaystyle\frac{1+\sqrt{5}}{2}$となる．