問題
方程式$\vert x^2-9\vert =3x+k$が異なる4つの実数解をもつとき,定数$k$のとり得る値の範囲は$\boxed{ }<k< \boxed{ } $である.
【関西大学 2014】
解答
方程式を変形すると
$\vert x^2-9\vert -3x=k$
この方程式の解の個数は,$y= \vert x^2-9\vert -3x$と直線$y=k$の交点の個数に等しい.
関数 $y= \vert x^2-9\vert -3x$ に関して
$x≦-3, 3≦x$のとき,
$y=x^2-3x-9=(x-\dfrac{3}{2})^2-\dfrac{45}{4}$
$-3<x<3$のとき,
$y=-x^2-3x+9=-(x+\dfrac{3}{2})^2+\dfrac{45}{4}$
したがって,関数 $y= \vert x^2-9\vert -3x$ のグラフは以下となる.
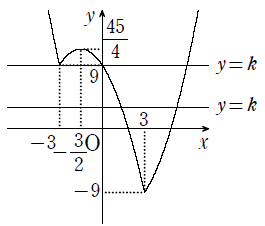
方程式$\vert x^2-9\vert =3x+k$が異なる4つの実数解をもつのは,上記グラフの交点が4つになるときであるので,求める$k$の値の範囲は
$9<k<\dfrac{45}{4}$



コメント