前編はこちらから
前編では主に因数分解をした後に、各項ごとに正負を判断する方法を紹介しました.ここまではしっかりマスターしてください!
威力を発揮するのは指数・対数関数、三角関数
前編でも紹介したが,数学IIIにおける代入することの苦しみがあるのは『指数・対数関数、三角関数』ではないだろうか.ここでは例題として,三角関数の問題を引用する.
例題
$0≦x≦\displaystyle\frac{\pi}{2}$ の範囲で関数$f(x)=\cos x\sin^2x$と$g(x)=\cos^3x$を考える.
(1) $f(x)$の極値を求めよ.ただし,$f(x)$が極値をとるときの$x$の値は求めなくてよい.
【信州大学 一部抜粋】
解き進めると・・・?
解答
(1) $f'(x)=-\sin x×\sin^2x+\cos x×2\sin x\cos x$
$=-\sin^3x+2\sin x\cos^2x$
$=-\sin^3x+2\sin x(1-\sin^2x)$
$=-\sin^3x+2\sin x(1-\sin^2x)$
$=\sin x(-\sin^2x+2-2\sin^2x)$
$=-\sin x(3\sin^2x-2)$
$=-\sin x(\sqrt{3}\sin x+\sqrt{2})(\sqrt{3}\sin x-\sqrt{2})$
となるんですよね.みなさんならここからどうする?
色々と方法はありますが,私が推したいのは『置き換えて,グラフを描く』ということです.
置き換えてグラフを描く
- 関数を$H(X)$とし,$X=\sin x$と置き換える
- $X$の範囲を求める.
- 定義域を守った$H(X)$のグラフを描く.
以上です.では実際に取り組みましょう.
$X=\sin x$と置き換え,関数$f'(x)=H(X)$とする.$0≦x≦\displaystyle\frac{\pi}{2}$とすると,$X$の範囲は$0≦X≦1$となる.
$H(X)=-X(\sqrt{3}X+\sqrt{2})(\sqrt{3}X-\sqrt{2})$
となる.ここで,$H(X)$と$X$軸の交点は$X=0, ±\displaystyle\frac{\sqrt{2}}{\sqrt{3}}$となる.$X$の範囲を満たす交点は$X=0, \displaystyle\frac{\sqrt{2}}{\sqrt{3}}$となる.
グラフは以下となる.
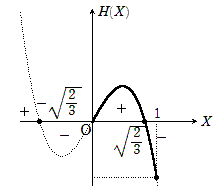
このグラフの正負と,増減表の$f'(x)$の正負は一致しています.このグラフなら簡単に描けますよね?(ただし,範囲が大きくなり,交点が増えると複雑化するので注意)
指数・対数関数でも効力を発揮するので是非試してみてください!




コメント