区分求積法　簡単積分化

区分求積法の公式は・・

➀$\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^{n}f(\displaystyle\frac{k}{n})=\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{n}\{f(\displaystyle\frac{1}{n})+f(\displaystyle\frac{2}{n})+\cdots+f(\displaystyle\frac{n}{n})\}$

　　　　　　　　　　$=\displaystyle\int_{0}^{1}f(x)dx$

➁$\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{n}\displaystyle\sum_{k=0}^{n-1}f(\displaystyle\frac{k}{n})=\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{n}\{f(0)+f(\displaystyle\frac{1}{n})+\cdots+f(\displaystyle\frac{n-1}{n})\}$

　　　　　　　　　　$=\displaystyle\int_{0}^{1}f(x)dx$

区分求積のイメージ

　公式➀、➁はともに

・関数$f(x)$の積分区間0→1を$n$等分した長方形の面積和である

・長方形の面積は（縦）×（横）となるので、$f(\displaystyle\frac{k}{n})×\displaystyle\frac{1}{n}$というものを足し合わせる

【グラフイメージ】

➀

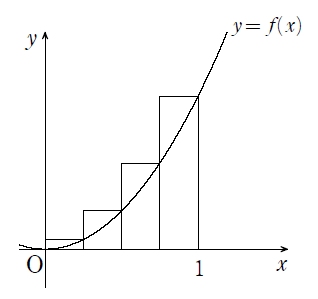
➁

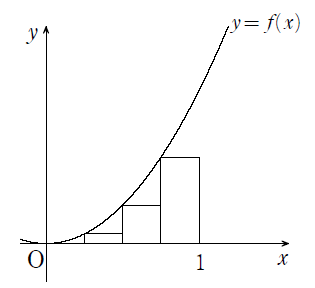
　➀，➁ともにグラフの面積からかけ離れているが，$n$等分している$n$の値がかなり大きくなる($\infty$に近づく）と誤差がなくなる（とみなすことができる）ため，積分しているのと同値とみなすことができる！というものである．

式処理の仕方

　積分区間は0→1だけだとお思いですか？そんなことはありません。ただしこれさえ覚えておけば式処理ができてしまいます。

　結論はこれです。

$\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{n}\displaystyle\sum_{k=△}^{●}f(\displaystyle\frac{k}{n})=\displaystyle\int_{△のnの係数}^{●のnの係数}f(x)dx$

(例1)　$\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{n}\displaystyle\sum_{k=n+1}^{2n}f(\displaystyle\frac{k}{n})=\displaystyle\int_{1}^{2}f(x)dx$

(例2)　$\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{n}\displaystyle\sum_{k=0}^{3n-1}f(\displaystyle\frac{k}{n})=\displaystyle\int_{0}^{3}f(x)dx$

どうですか？少しでもイメージをつかむことができましたか？