区分求積法 攻略
昨日の記事を見られていない方はこちらから・・
問題
極限値$\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{\sqrt{n}}\displaystyle\sum_{k=1}^{n}\displaystyle\frac{1}{\sqrt{n+k}}$を求めよ.
【青山学院大学 2020】
解答
$\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{\sqrt{n}}\displaystyle\sum_{k=1}^{n}\displaystyle\frac{1}{\sqrt{n+k}}=\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^{n}\displaystyle\frac{1}{\sqrt{1+\displaystyle\frac{k}{n}}}$
$=\displaystyle\int_{0}^{1}\displaystyle\frac{1}{\sqrt{1+x}}dx$
$=\displaystyle\int_{0}^{1}(1+x)^{-\frac{1}{2}}dx$
$=[2(1+x)^{\frac{1}{2}}]_{0}^{1}$
$=2\sqrt2-2$
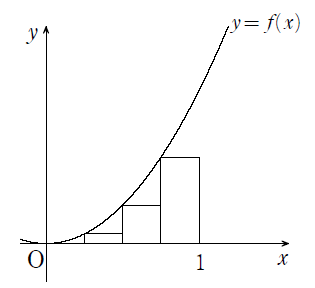


コメント