導入
しつこい区分求積法攻めは本日で終了です.区分求積法の問題とわかるから解ける問題もあるということです.それが今日の問題です.どうすればこの問題が区分求積法の問題と結びつくのかを自分なりに考えましょう.
私的には、和と積はlogを使うことで自在に操ることができるということがあるということ.また,長方形の面積公式は縦×横というものがありますが、横にあたる$\displaystyle\frac{1}{n}$という値($n$等分)が存在することも反応する鍵ではないでしょうか.
問題
極限値$\displaystyle\lim_{n \to \infty}\dfrac{1}{n}\sqrt[n]{(n+1)(n+2)\cdot\cdots\cdot(n+n)}$
【早稲田大学 2020】
解答
自然対数を考える.
$\log\{\dfrac{1}{n}\sqrt[n]{(n+1)(n+2)\cdot\cdots\cdot(n+n)}\}$
$=\dfrac{1}{n}\log(\dfrac{n+1}{n}\cdot\dfrac{n+2}{n}\cdot\cdots\cdot\dfrac{n+n}{n})$
$=\dfrac{1}{n}\displaystyle\sum_{k=1}^{n}\log(1+\dfrac{k}{n})$
となる.
$=\displaystyle\lim_{n \to \infty}\log\lbrace\dfrac{1}{n}\sqrt[n]{(n+1)(n+2)\cdot\cdots\cdot(n+n)}\}$
$=\displaystyle\lim_{n \to \infty}\dfrac{1}{n}\sum_{k=1}^{n}\log(1+\dfrac{k}{n})$
$=\displaystyle\int_{0}^{1}\log(1+x)dx$
$=[(x+1)\log(x+1)]_{0}^{1}-\displaystyle\int_{0}^{1}dx$
$=2\log 2-1$
$=\log\dfrac{4}{e}$
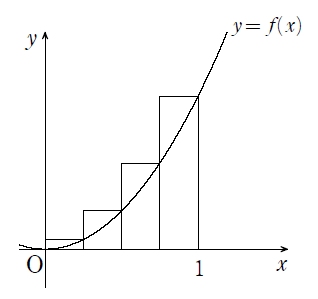


コメント