前回は
(1)はこちらに記載しております。積分方程式シリーズも大詰めですね。まとめを作成していけたらいいのですが(;´・ω・)・・・
問題
(2) $a$,$b$を実数とする.$g(x)=ae^x+b\displaystyle\int_{0}^{1}tg(t)dt$を満たす関数$g(x)$が存在しないような点$(a, b)$全体の集合を図示せよ.
【和歌山大学 2020】
解答
(2) $g(x)=ae^x+b\displaystyle\int_{0}^{1}tg(t)dt \cdots④$
ここで,
$B=\displaystyle\int_{0}^{1}tg(t)dt \cdots➄$
とすると,④は
$g(x)=ae^x+bB \cdots➅$
となる。このとき,
$\displaystyle\int_{0}^{1}tg(t)dt=\displaystyle\int_{0}^{1}(ate^t+bBt)dt$
$=[a(te^t-e^t)+\displaystyle\frac{1}{2}bBt^2]_{0}^{1}$
$=\displaystyle\frac{1}{2}bB+a$
となるので,➄より,
$a=\displaystyle\frac{1}{2}bB+a$
$(2-b)B=2a \cdots⑦$
④をいたす関数$g(x)$が存在しない条件は,⑦を満たす$B$が存在しないことである.すなわち,
$2-b=0$かつ$2a≠0$
よって,
$b=2$かつ$a≠0$
であるから,点$(a, b)$全体の集合は下図の太線部(○部を除く)となる.
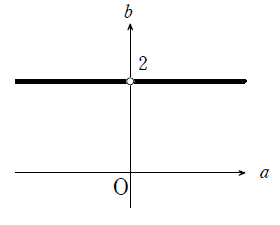




コメント